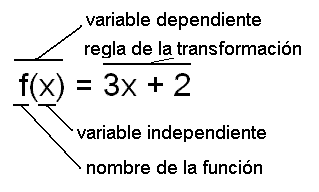
La primera condición es la de existencia que significa que cada elemento del dominio de la relación debe estar relacionado con un elemento del conjunto de llegada de la relación. Formalmente se define así: Sea f una relación de dominio A y de conjunto llegada B. Si cumple la condición de existencia, entonces para todo x de A, existe un y tal que (x,y) es elemento de F.
La segunda condición es la de unicidad, implica que cada elemento de A está relacionado con solo un elemento de B. Se define así: Si (x,y) elemento de f y (x,z) elemento de f, implica que y=z. O sea, un elemento x de A no puede estar relacionado con dos elementos distintos de B.